Circuit analysis Tutorial
AKNM Circuit Magic- circuit analysis software
Node Voltage Method
The node voltage method is deduced from the Kirchhoff’s current law (KCL) and Ohm’s
laws
The following formulas are used to solve circuit.
where
Node i conductivity is the sum of
conductivities of all branches which connected with Node i.
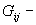Node i to node j conductivity is the
negative sum of conductivities of all branches which connect Node i with Node j.
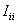.Node i - current
Sample: Circuit Solution By Node Voltage
Step 1. Construct following circuit using circuit editor.
Step 2. Run solution by node voltage method.
Step 3. Correct following solution.
Electrical scheme
Initial variables
R
1=10 ohms; R2=20 ohms; R3=25 ohms; R4=10 ohms; R5=10 ohms;
E
1=10V; E2=15V;
J
1=10A;
Solution
V
1·G11+V2·G12+V3·G13=I11
V
1·G21+V2·G22+V3·G23=I22
V
1·G31+V2·G32+V3·G33=I33
Node 1 conductivity
G11=1/R2+1/R1+1/R4=0,25
Node 1 to Node 2 conductivity
G12=-1/R2=-0,05
G13=-1/R1=-0,1
G22=1/R2+1/R5=0,15
G23=-1/R5=-0,1
G33=1/R5+1/R1+1/R3=0,24
I11=-E2/R1=-1,5
I22=-J1=-10
I33=E2/R1-E1/R3=1,1
Linear equations
0,25V1-0,05V2-0,1V3=-1,5
-0,05V1+0,15V2-0,1V3=-10
-0,1V1-0,1V2+0,24V3=1,1
V1=-69,706
V2=-147,06
V3=-85,735
V4=0
Branch currents calculation using Ohm’s Law
I1=(V1-V2)/R2=3,86765
I2=(V2-V3)/R5=-6,13235
I3=(V1-V3+E2)/R1=3,10294
I4=J1=10
I5=(V3-V4+E1)/R3=-3,02941
I6=(V1-V4)/R4=-6,97059
